THIS APPLICATION NOTE
- Gives a brief orientation of simple timing analysis measurements on clock signals
- Explains how to interpret timing and jitter measurements
- Gives examples of measurements on non-modulated clocks, spreadspectrum clocks, serial data with embedded clock, and clocked data
- Explains how advanced jitter measurements can improve timing characterization and troubleshooting
This application note uses the 5 Series MSO mixed signal oscilloscope to illustrate jitter measurements. The 6 Series MSO operates identically, but is available with higher bandwidth and offers lower input noise. Many of the measurements shown can be performed with other oscilloscopes, although specific setups will vary. Some of the measurements in this application note take advantage of the optional Advanced Jitter Analysis application for the 5 and 6 Series MSOs.
Introduction
Clocks are the heartbeats of embedded systems, providing timing references and synchronization between components, subsystems, and entire systems. Disruptions and distortions of clock signals can cause degraded or intermittent system operation, so thorough characterization of clock signals is a critical step in reliable embedded system design.
Jitter is a common way to express the performance of a clock circuit. Put simply, jitter is the deviation of the timing of a signal edge from where it should be. There are a variety of measurements to characterize jitter.
This application note provides several examples of jitter measurements using the standard and optional measurement capabilities available in the 5 and 6 Series MSOs.
Clock Jitter Characterization
USING STANDARD AUTOMATED MEASUREMENTS
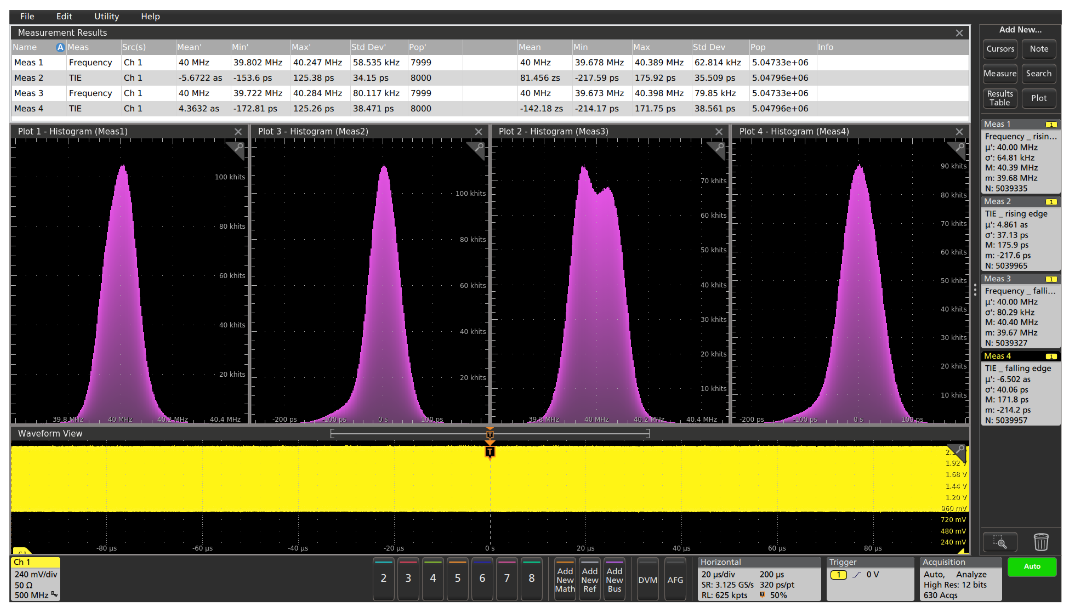
Standard automated measurements provide a good starting point for jitter analysis, verifying that the clock frequency is meeting specifications. Adding measurement statistics, such as minimum and maximum frequency, provides confidence that the clock pulses are continuous. The standard deviation (σ) provides a quantitative measure of the frequency stability. However, these statistics give little insight into the manner of frequency variation. Graphical tools such as measurement histograms give more information about the characteristics of the measurement variations.
The Frequency and Time Interval Error (TIE) measurements, shown in Figure 1, are made on the rising and falling edges of every cycle of every acquisition of the 40 MHz clock signal. These timing measurements are made relative to the average clock frequency in the acquisition. The statistics in the measurement badges at the right side of the display and in the results table at the top of the display help to characterize the variations of these measurements over time. The statistics at the left side of the results table represent the current acquisition, while the statistics at the right side represent the accumulation of all acquisitions made over time.
The two histograms on the left represent the frequency and TIE measurement values on the rising edges of the clock, helping you to understand the timing variations. In this case, the distributions appear to be fairly Gaussian, suggesting that the jitter is predominantly random.
However, the two histograms on the right represent the frequency and TIE measurement values on the falling edges of the clock. Interestingly, the shape of the histogram of the frequency measurements appears to be significantly different, suggesting that further investigation is warranted.
All of the analysis shown in Figure 1 is based on the standard capabilities of the 5 Series MSO. For deeper analysis of the timing variations, the optional Advanced Jitter and Timing Measurements can be used.
USING ADVANCED JITTER ANALYSIS
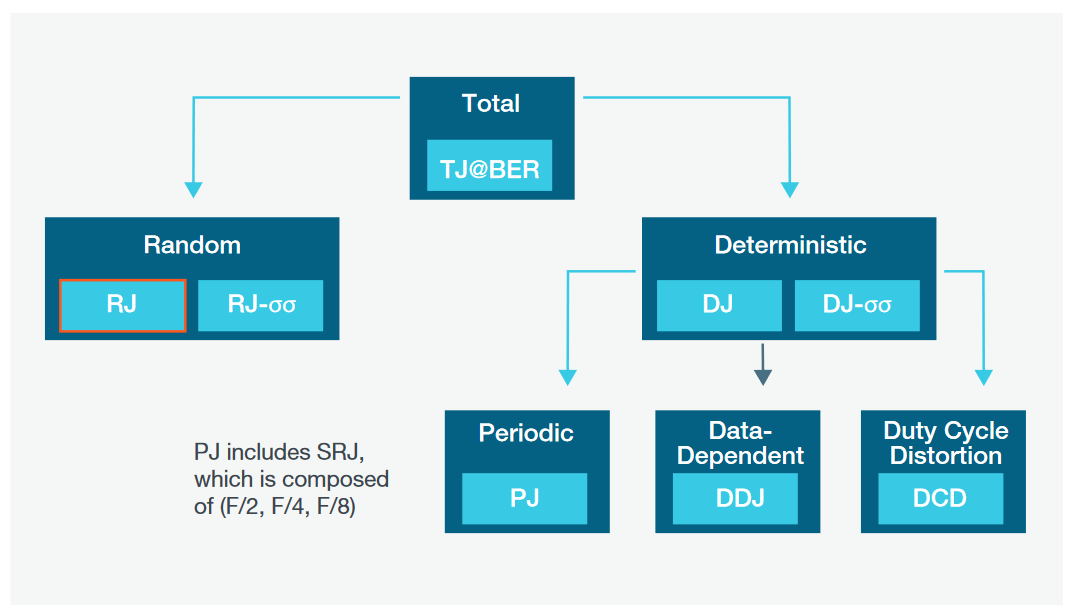
As shown in Figure 2, timing jitter can be decomposed into a number of components, providing insight into the root cause of the timing variations. For the rest of this application note, we’ll look at some practical examples using the Advanced Jitter Measurements in the 5 Series MSO to demonstrate jitter decomposition and interpretation of the results.
40 MHZ NON-MODULATED CLOCK REVISITED
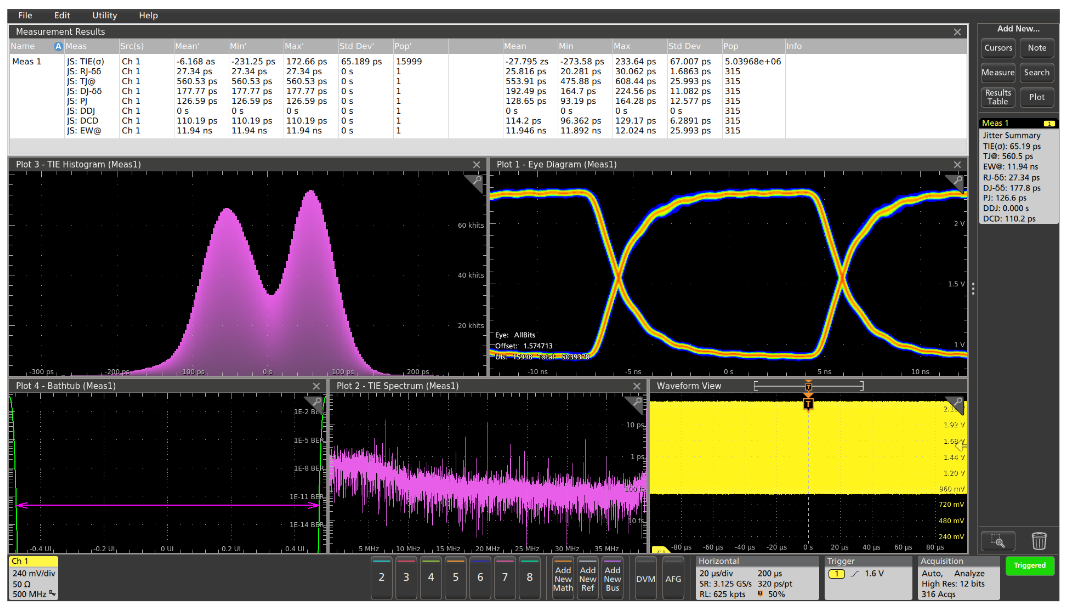
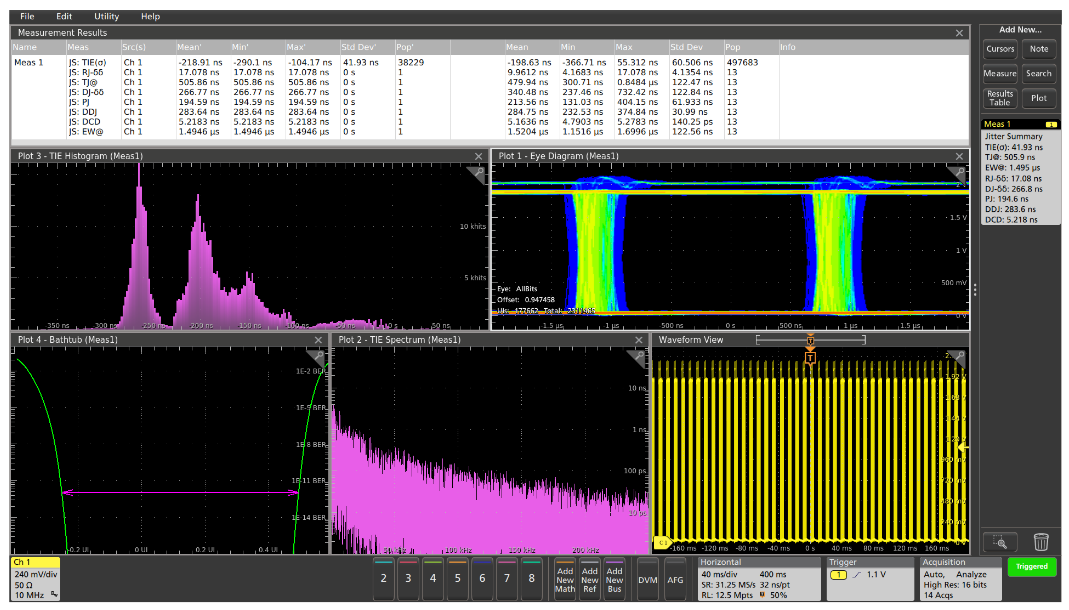
Applying the Jitter Summary measurement group in the 5 Series MSO’s optional Advanced Jitter Measurements to the 40 MHz clock example shown in Figure 1 reveals some new clues. The Jitter Summary measurement in Figure 3 renders an eye diagram of the signal, measures TIE, plots the histogram and spectrum of the TIE measurement, and decomposes the jitter into its individual components.
At first glance, the open eye in the eye diagram in Figure 3 suggests that the clock signal has fairly low jitter. Indeed, the Total Jitter (TJ@BER) measurement value of about 554 ps is about 2.2% of the 40 MHz clock period. The jitter decomposition shows that the Random Jitter component (RJ-δδ) is a very small part of the total jitter.
Therefore, the Deterministic Jitter (DJ-δδ) must be the dominant component. The bi-modal nature of the TIE histogram also suggests a strong deterministic jitter component. The DJ is further decomposed into Periodic Jitter, Data Dependent Jitter, and Duty Cycle Distortion.
The Periodic Jitter (PJ) is about a quarter of the jitter. There are clear spectral components in the TIE Spectrum plot, indicating strong peaks at 7, 17, and 32 MHz, which suggests that the jitter has significant uncorrelated deterministic jitter, perhaps caused by signal crosstalk on the circuit board or within the FPGA. Since this is a clock signal rather than a data signal, the Data Dependent Jitter (DDJ) is zero. The Duty Cycle Distortion (DCD) also makes up about a fifth of the total jitter, suggesting that the clock shaping circuit deserves further analysis and optimization.
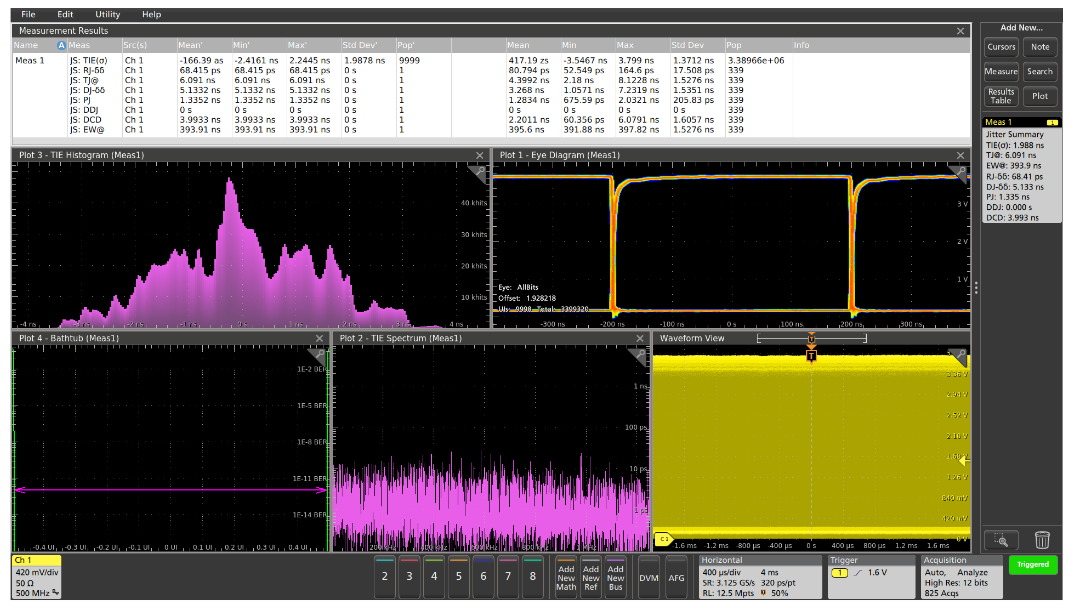
Figure 4 shows the analysis of another clock signal in the system, and it exhibits some different jitter characteristics. From the open eye in the eye diagram, you can conclude that the jitter on the clock signal is small. This is verified by the Total Jitter measurement value of about 4.4 ns which is less than 0.55% of the clock period. The jitter decomposition shows that the Random Jitter component is a very small part of the total jitter. The Periodic Jitter is also relatively small, and there are no clear spectral components in the TIE Spectrum plot, indicating that the jitter on the signal is not significantly related to uncorrelated components of the deterministic jitter. And, since this is a clock signal rather than a data signal, the Data Dependent Jitter is zero. However, the Duty Cycle Distortion makes up a significant part of the total jitter.
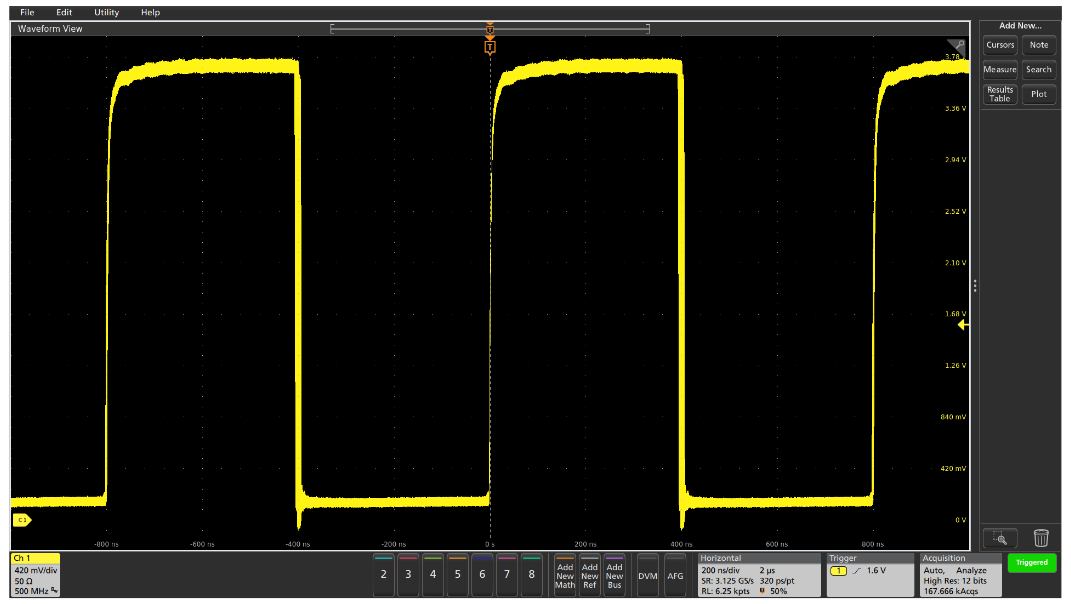
Armed with this clue, Figure 5 shows a persistence display of the clock signal, where the wide falling edges of the signal clearly show that the duty cycle is varying significantly. If the embedded system uses the rising edge of the clock throughout, this duty cycle variation may not present a problem. However, if some of the circuits depend upon the rising edge and others use the falling edge, this jitter may cause the system to behave incorrectly or unreliably
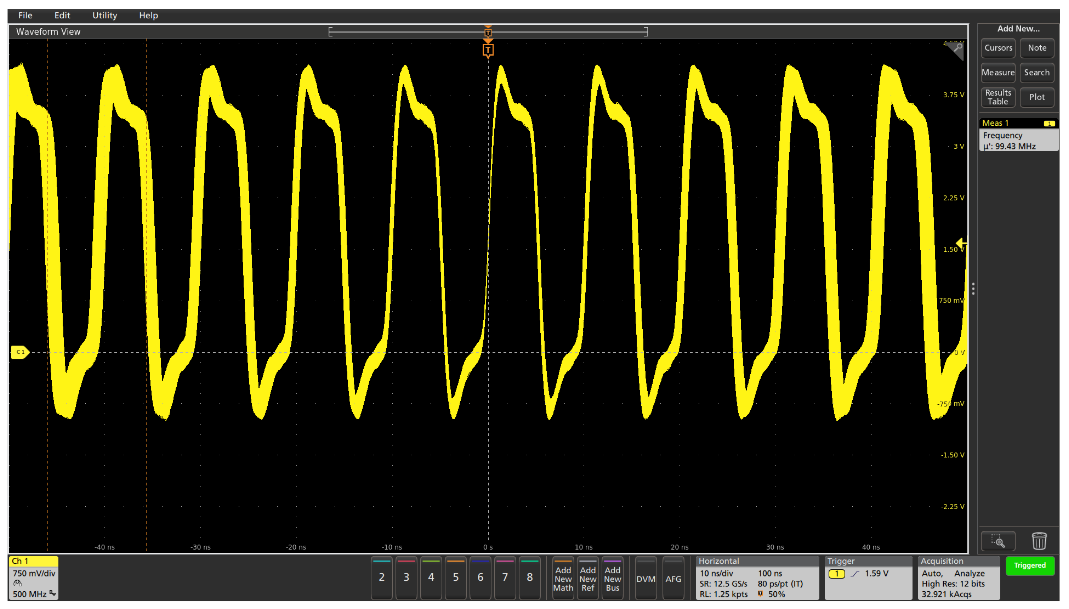
Spread Spectrum Clock Characterization
The final example of clock analysis in this design is shown in Figure 6. The frequency measurement varies over time from about 97 MHz to about 100 MHz, and the clock period is varying, as indicated by the horizontal smearing in the waveform away from the trigger point.
Adding measurement statistics could help quantify how much the frequency is varying, and could help verify that the clock’s frequency is within design specifications, but it would not help in understanding how frequency is varying. In this case, the signal is a spread-spectrum clock where the frequency is intentionally modulated. But is the design working as expected? Again, the Jitter Summary provides a wealth of information. As expected and desired, the frequency variations (jitter) are dominated by Periodic Jitter, reflected in the measurement results table at the top of the display and in the saddle-shaped TIE histogram.
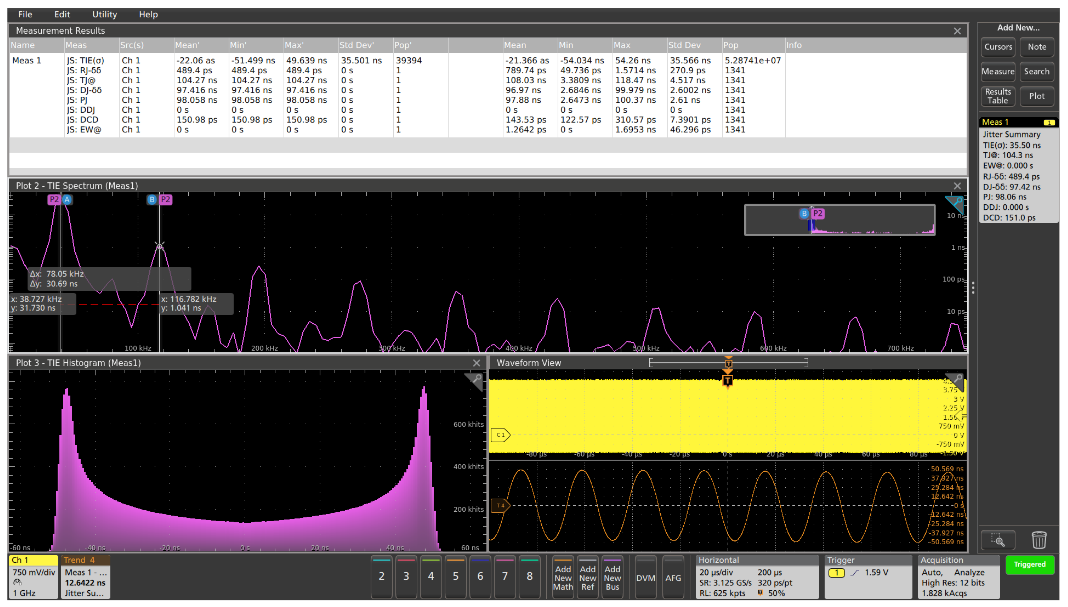
The Time Interval Error caused by the modulation can be viewed in the orange time trend in the lower right corner of the display. From the TIE time trend waveform and the cursor measurements on the peaks of the TIE Spectrum in the middle of the display, we can see that the modulation rate is about 39 kHz.
The shape of the spectrum, dominated by odd harmonics with rapidly decreasing magnitudes, suggests that the modulation is likely a square or triangular waveform. But the TIE is the integral of the actual modulation signal, so we can conclude that the spread spectrum clock is likely modulated with a 39 kHz triangle wave.
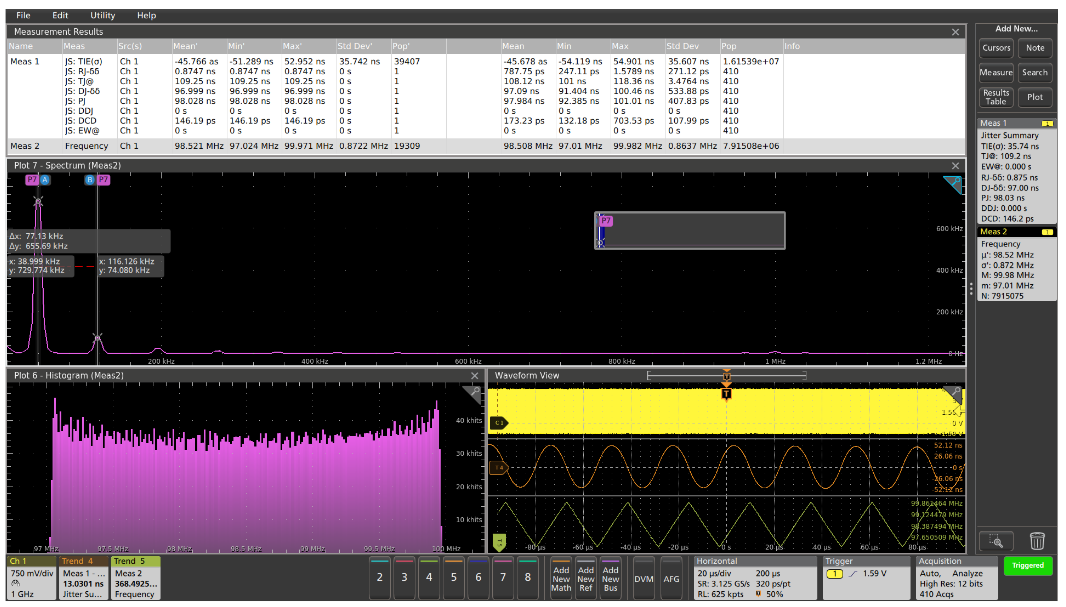
To verify this theory, we turn on the frequency measurement and plot the measurement histogram, spectrum, and time trend. With cursor measurements on the spectrum, we verify that the modulation indeed is a 39 kHz triangle wave. The measurement histogram is flat from 97 to 100 MHz, as expected, and the time trend provides another view of the same modulation.
Low-speed Serial Bus Jitter Measurements
Jitter also affects the performance of serial buses including self-clocking buses. Figure 9 shows the Jitter Summary analysis of a 500 kb/s differential CAN bus signal at the transmitter. Similar measurement techniques can be used on other serial buses, at the transmitter and the receiver.
The first step in this analysis is to recover a clock signal from the serial data signal. In this case, the software is performing a clock recovery using a Phase Locked Loop (PLL) with a narrow loop bandwidth to remain locked between data bursts. This recovered clock is then used as the reference for the jitter analysis.
The jitter decomposition shows that the majority of the total jitter at the transmitter is due to Data Dependent Jitter, and the random and duty cycle dependent components are very small. There is also a considerable Periodic Jitter component which appears to be related to the amplitude modulation of the signal at the beginning of each of the data bursts (but not related to the individual data bits), which is visible in the eye diagram and time-domain displays.
Clocked Data Jitter Measurements
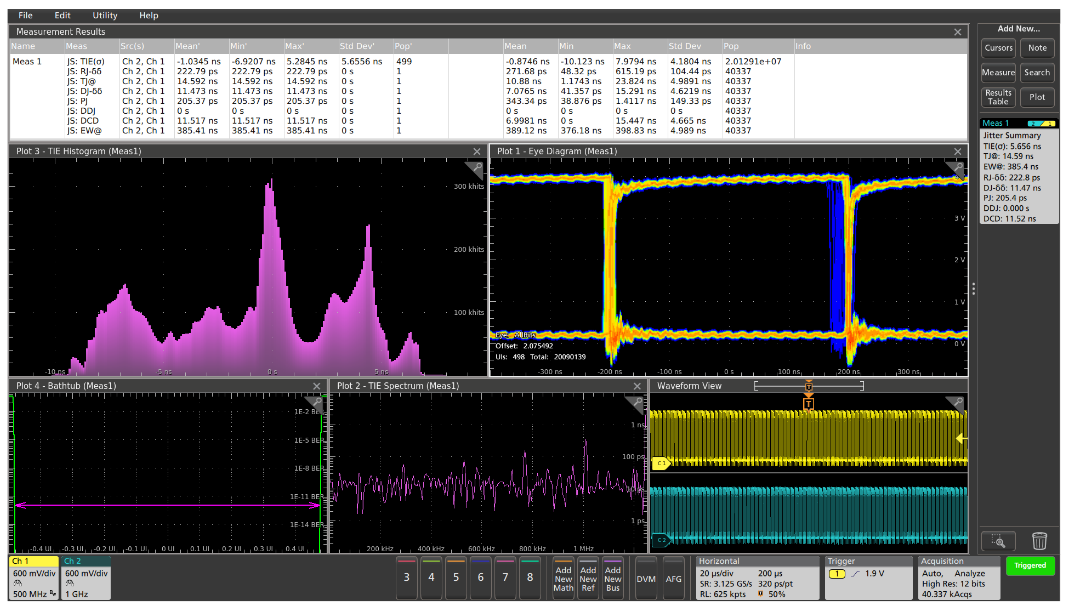
The final example of jitter analysis is on a synchronous logic circuit. Unlike the previous examples, this circuit has an explicit clock signal, so the jitter measurements are made on the cyan data signal on channel 2 relative to the yellow clock signal on channel 1 (shown in the lower right corner of Figure 10).
The clock rate is just 1.25 MHz and the circuit board traces are short, so the signals are fairly clean, as indicated by the low random jitter and wide eye pattern. Because this circuit is using a separate clock signal, we would not expect that the jitter would be data-dependent.
In this case, the jitter seems to be dominated by duty cycle distortion. Further analysis of the circuit shows that the clock for this circuit was derived from the clock that was shown in Figure 5. Not coincidentally, a significant portion of this circuit’s total jitter is due to the duty cycle distortion of the clock signal.


